Простыми словами о преобразовании фурье. Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих

Эти преобразования являются функциональными, так как они преобразовывают некоторую функцию переменного в совершенно иную функцию переменного , и наоборот.

Преобразования Фурье имеют вид:

Интегральное уравнение (4.34) называется прямым, а уравнение (4.35) - обратным преобразованием Фурье. Сокращенная форма записи этих уравнений

Интеграл Фурье (прямое преобразование Фурье) позволяет разложить непериодическую функцию обладающую свойством абсолютной интегрируемости в заданных пределах, в бесконечный ряд гармоник, образующих непрерывный спектр частот в интервале от до с бесконечно малым интервалом частот между смежными гармониками (т. е. в пределе

Метод преобразования Фурье непригоден при ненулевых начальных (или граничных) условиях. Этот метод может применяться лишь тогда, когда искомые функции имеют изображение Фурье, т. е. для абсолютно интегрируемых функций времени, удовлетворяющих неравенству

Наиболее часто встречающимися в теории регулирования функциями являются единичная ступенчатая функция (1.44) и произведение синусоидальной функции на единичную функцию (1.51). Преобразование Фурье неприменимо ни к одной из этих функций, так как не удовлетворяется условие (4.38).

Указанные недостатки ограничивают использование метода преобразования Фурье.

Чтобы применить интеграл Фурье, необходимо выбрать функцию, Достаточно близкую к исследуемой, например, к ступенчатой функции при конечных значениях но в то же время удовлетворяющую условию (4.38). Такую функцию можно получить, умножив

ступенчатую функцию на где с - достаточно малая положительная величина. Вновь полученная вспомогательная функция

Устремляя с к нулю и делая предельный переход, можно от вспомогательной функции перейти к основной Кроме того, если ограничиться функциями , тождественно равными нулю при то для большого класса функций будет справедливо условие (4.38) и можно найти частотный спектр функции, используя выражение (4.34). Вместо введем новое обозначение так как эта величина теперь зависит и от с:

Положив с находим

Эта формула совпадает с прямым преобразованием Лапласа (4.9).

Отсюда следует, что преобразование Фурье можно рассматривать как частный случай преобразования Лапласа.

Изложенные выше методы преобразований позволяют сделать следующие заключения:

1) интегро-дифференциальные уравнения заменяются алгебраическими уравнениями;

2) отпадает операция определения постоянных интегрирования, так как начальные условия учитываются с самого начала при нахождении изображения искомой величины;

3) операция определения корней характеристического уравнения полностью сохраняется.

Наиболее удобным для решения практических задач является метод преобразования Лапласа. В несколько измененной форме он может быть применен к исследованию дискретных САУ (см. гл. 7).

Рассмотрим использование метода преобразований Лапласа для решения дифференциального уравнения вида

Преобразуем это дифференциальное уравнение, используя прямое преобразование Лапласа (4.9) и теоремы 1 и 2. В результате получим алгебраическое уравнение, записанное для изображений:

где - сумма всех членов, содержащих начальные условия.

Отсюда находится изображение искомой функции

При нулевых начальных условиях выражения (4.41) и (4.42) упрощаются:

Зная изображение искомой функции можно найти оригинал например, по таблицам изображений.

Если изображение искомой величины представляет собой рациональную алгебраическую дробь, то ее стараются записать в виде суммы простых дробей с постоянными коэффициентами. Обратное преобразование для каждой из этих простых дробей может быть получено из таблиц, а окончательное выражение оригинала представлено как сумма отдельных найденных значений. Для определения оригинала можно также воспользоваться теоремой разложения.

Если изображение Лапласа представляет собой рациональную алгебраическую дробь вида

Рассмотрим основные свойства преобразования Фурье.

Линейность . Рассмотрим функции и
, имеющие спектры
и
:

(12)

Тогда спектр их линейной комбинации будет:

Задержка во времени . Считаем, что известен спектр
сигнала

(14)

Рассчитаем спектр сигнала, сдвинутого во времени:
. Обозначим аргумент функции новой переменной
, тогда
и

Получили, что задержка сигнала на время приводит к умножению спектра на
.

Изменение масштаба. Считаем, что известен спектр
сигнала
, как через
выражается спектр сигнала
. Вводим новую переменную
, делаем замену переменной интегрирования
.

(16)

Умножение на
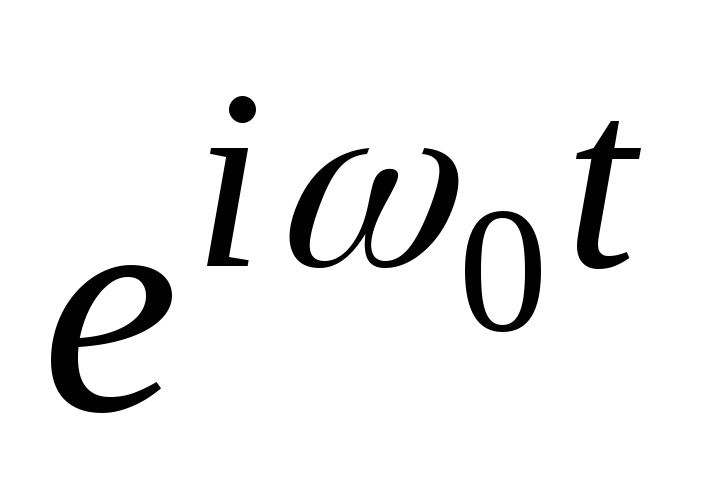. Как и в предыдущем случае, считаем, что известен спектр
сигнала
. Найдем спектр этого сигнала, умноженного на
.

Таким образом, умножение сигнала на
приводит к смещению спектра на.

Спектр производной. В данном случае ключевым моментом является абсолютная интегрируемость функции. Из того, что интеграл от модуля функции должен быть ограничен, следует, что на бесконечности функция должна стремиться к нулю. Интеграл от производной функции берётся по частям, получившиеся внеинтегральные слагаемые равны нулю, так как на бесконечности функция стремится к нулю.

(18)

Спектр интеграла. Найдем спектр сигнала
. Причём будем считать, что
, то есть у сигнала отсутствует постоянная составляющая. Это требование необходимо, чтобы внеинтегральные слагаемые были равны нулю, когда интеграл берётся по частям.

(19)

Теорема о свёртке. Известно, что
и
спектры функций
и
соответственно. Требуется выразить спектр свертки
через
и
. Для этого в интеграле Фурье от свёртки у одной из функций выполним замену переменой
, тогда в показателе экспоненты можно сделать замену
. В результате такой замены двукратный интеграл будет равен произведению двух интегралов Фурье.

(20)

Преобразование Фурье свёртки двух сигналов даёт произведение спектров этих сигналов.

Произведение сигналов. Известно, что
и
– спектры функций
и
соответственно. Требуется выразить спектр произведения
через спектры
и
. Подставим в интеграл Фурье вместо одного из сигналов, например
, его выражение через обратное преобразование Фурье, а потом поменяем порядок интегрирования.

(21)

Спектр произведения сигналов есть свёртка спектров этих сигналов.

Спектр дискретного сигнала

Особое внимание стоит уделить дискретным сигналам, так как именно такие сигналы используются в цифровой обработке. Дискретный сигнал в отличие от непрерывного является последовательностью чисел, соответствующих значениям непрерывного сигнала в определённые моменты времени. Условно дискретный сигнал можно рассматривать как непрерывный сигнал, который в определённые моменты времени принимает какие-то значения, а в остальное время равен нулю. Таким образом, например, дискретный
сигнал может быть задан как произведение непрерывного сигнала
на последовательность периодически повторяющихся прямоугольных импульсов
– тактирующих импульсов (рис.1).

Рис. 1. Дискретизация сигнала.

(22)

Прямоугольные импульсы имеют длительность , период повторения:

(23)

Амплитуда импульса выбрана таким образом, чтобы интеграл импульса по периоду равнялся . При этом тактирующие импульсы безразмерны. Разложим последовательность таких импульсов в тригонометрический ряд:

(24)

Чтобы получить мгновенные отсчёты сигнала
, надо устремить длительность импульсов к нулю:
. Такой тактирующий сигнал назовём идеальным. При этом коэффициенты разложения
в ряд Фурье все будут равны 1.

(25)

Точно такой же вид имеет разложение в ряд Фурье функции:

(26)

Коэффициенты разложения в тригонометрический ряд тактирующего сигнала
:

(27)

Тогда дискретный сигнал будет иметь вид:

При вычислении преобразования Фурье дискретного сигнала меняем местами операцию суммировании и интегрирования, а потом используем свойство δ -функции:

Спектр дискретного сигнала является периодической функцией. Рассмотрим экспоненту в отельном слагаемом
как функцию частоты. Её период повторения равен. Самый большой период повторения у слагаемых с номерами
, и это, соответственно, будет периодом повторения всего спектра. То есть спектр дискретного сигнала имеет период повторения, равный частоте квантования
.

Получим ещё одно представление
. В силу того, что
является произведением функций
и
, спектр дискретного сигнала
вычисляется как свёртка спектров непрерывного сигнала
и спектра тактирующего сигнала
.

(30)

Вычислим
, используя (25). Так как
периодическая функция, её спектр дискретный.

Таким образом, свёртка (30)

Из выражения (32) следует, что спектр дискретного сигнала представляет собой периодически повторяющуюся функцию
.

Сам факт того, что в результате дискретизации в спектре сигнала происходят качественные изменения, говорит о том, что исходный сигнал может быть искажён, так как он полностью определяется своим спектром. Однако с другой стороны периодическое повторение одного и того же спектра само по себе не вносит ничего нового в спектр, поэтому при определённых условиях, зная значения сигнала в отдельные моменты времени, можно найти какое значение этот сигнал принимал в любой другой момент времени, то есть получить исходный непрерывный сигнал. В этом состоит смысл теоремы Котельникова, которая накладывает условие на выбор частоты квантования в соответствии с максимальной частотой в спектре сигнала.

Если это условие нарушено, то после оцифровки сигнала произойдёт наложение периодически повторяющегося спектра (рис. 2). Получившийся в результате наложения спектр будет соответствовать другому сигналу.

Рис. 2. Перекрывание спектров.

Одним из мощных средств исследования задач математической физики является метод интегральных преобразований. Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(x) называется функция где К(х, ш) - фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существуете собственном или несобственном смысле). §1. Интеграл Фурье Всякая функция f(x), которая на отрезке [-f, I] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом Коэффициенты а*, и 6„ ряда (1) определяются по формулам Эйлера-Фурье: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения Ряд в правой части равенства (1) можно записать в иной форме. С этой целью внесем в него из формул (2) значения коэффициентов а» и оп, подведем под знаки интегралов cos ^ х и sin х (что возможно, поскольку переменной интегрирования является т) О) и используем формулу для косинуса разности. Будем иметь Если функция/(ж) первоначально была определена на интервале числовой оси, большем, чем отрезок [-1,1] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-1,1] и продолжит се на всю числовую ось как периодическую функцию с периодом 21 (рис. 1). Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при I +оо. При этом естественно потребовать выполнения следующих условий: 1. f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох\ 2. функция f(x) абсолютно интегрируема на всей числовой оси, При выполнении условия 2 первое слагаемое правой части равенства (3) при I -* +оо стремится к нулю. В самом деле, Попытаемся установить, во что перейдет в пределе при I +оо сумма в правой, части (3). Положим так, что Тогда сумма в правой части (3) примет вид В силу абсолютной сходимости интеграла эта сумма при больших I мало отличается от выражения которое напоминает интегральную сумму для функции переменного £ составленную для интервала (0, +оо) изменения Поэтому естественно ожидать, что при сумма (5) перейдет в интеграл Сдругой стороны, при фиксировано) из формулы (3) вытекает, что и мы получаем равенство Достаточное условие справедливости формулы (7) выражается следующей теоремой. Теорема 1. Если функция f(x) абсолютно интегрируема на всей числовой оси и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке [а, 6], то справедливо равенство При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции /(ж), значение интеграла в правой части (7) равно Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл - интегралом Фурье. Если воспользоваться формулой дня косинуса разности, то формулу (7) можно записать в виде Функции а(£), Ь(£) являются аналогами соответствующих коэффициентов Фурье ап и Ьп 2тг-периодической функции, но последние определены для дискретных значений п, вто время как а(0> НО определеныдля непрерывных значений £ G (-оо, +оо). Комплексная форма интеграла Фурье Предполагая /(х) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл Этот интеграл равномерно сходится для, так как и потому представляет собой непрерывную и, очевидно, нечетную функцию от Но тогда С другой стороны, интеграл есть четная функция переменной так что Поэтому интегральную формулу Фурье можно записать так: Умножим равенство на мнимую единицу i и прибавим к равенству (10). Получим откуда, в силу формулы Эйлера будем иметь Это - комплексная форма интеграла Фурье. Здесь внешнее интегрирование по £ понимается в смысле главного значения по Коши: §2. Преобразование Фурье. Косинус- и синус-преобразования Фурье Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси. Определение. Функция откуда, в силу формулы Эйлера, будем иметь называется преобразованием Фурье функции /(г) (спектральной функцией). Это - интегральное преобразование функции /(г) на интервале (-оо,+оо) с ядром Используя интегральную формулу Фурье получаем Это так называемое обратное преобразование Фурье, дающее переход от F(£) к /(х). Иногда прямое преобразование Фурье задают так: Тогда обратное преобразование Фурье определится формулой Преобразование Фурье функции /(ж) определяют также следующим образом: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения Тогда, в свою очередь, При этом положение множителя ^ достаточно произвольно: он может входить либо в формулу (1"), либо в формулу (2"). Пример 1. Найти преобразование Фурье функции -4 Имеем Это равенство допуска ет дифференцирование по £ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда { принадлежит любому конечному отрезку): Интегрируя по частям, будем иметь Внеинтегральное слагаемое обращается в нуль, и мы получаем откуда (С - постоянная интегрирования). Полагая в (4) £ = 0, найдем С = F(0). В силу (3) имеем Известно, что В частности, для) получаем, что Пример 2 (разред кокдемсетора через сопропиление). Рассмотрим функцию 4 Для спектрам ыюй функции F(£) получаем Отсюда (рис.2). Условие абсолютной интегри-руемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как) = cos ж, f(x) = е1, для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует. Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| -+ +оо (как в примерах 1 и 2). 2.1. Косинус- и синус-преобразования Фурье Используя формулу косинуса, разности, перепишем интегральную формулу Фурье в следующем виде: Пусть f(x) - четная функция. Тогда так что изравснства (5) имеем В случае нечетной f(x) аналогично получаем Если f(x) задана лишь на (0, -foo), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) - нечетным. (7) Определение. Функция называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x) Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc(£). Иными словами, функции / и Fc являются взаимными косинус-преобразованиями. Определение. Функция называется синус-преобразованием Фурье функции f(x). Из (7) получаем, что для нечетной функции f(x) т.е. f и Fs являются взаимными синус-преобразованиями. Пример 3 (прамоугольный импульс}. Пусть f(t) - четная функция, определенная следующим образом: (рис. 3). Воспользуемся полученным результатом для вычисления интеграла В силу формулы (9) имеем Рис.3 0 0 В точке t = 0 функция f(t) непрерывна и равна единице. Поэтому из (12") получим 2.2. Амплитудный и фазовый спектры интеграла Фурье Пусть периодическая с периодом 2т функция /(х) разлагается в ряд Фурье Это равенство можно записать в виде где - амплитуда колебания с частотой п, - фаза. На этом пути мы приходим к понятиям амплитудного и фазового спектров периодической функции. Для непериодической функции f{x), заданной на (-оо, +оо), при определенньк условиях оказывается возможным представить ее интегралом Фурье осуществляющим разложение этой функции по всем частотам (разложение по непрерывному спектру частот). Определение. Спектральной функцией, или спектральной плотностью интеграла Фурье, называется выражение (прямое преобразование Фурье функции f называется амплитудным спектром, а функция Ф«) = -агgSfc) - фазовым спектром функции /(«). Амплитудный спектр.А(£) служит мерой вклада частоты £ в функцию /(ж). Пример 4. Найти амплитудный и фазовый спектры функции 4 Находим спектральную функцию Отсюда Графики этих функций изображены на рис. 4. §3. Свойства преобразования Фурье 1. Линейность. Если и G(0 - преобразования Фурье функций /(х) и д(х) соответственно, то при любых постоянных а и р преобразованием Фурье функции a f{x) + р д(х) будет функция a Пользуясь свойством линейности интеграла, имеем Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через будем писать. Если F(£) есть преобразование Фурье абсолютно интегрируемой на всей числовой оси функции /(ж), то F(() ограничена при всех. Пусть функция f(x) абсолютно интегрируема на всей оси - преобразование Фурье функции f(x). Тогда 3«fltsJ. Пусть f(x) - функция, допуска кнцэя преобразование Фурье, Л - дойств ительяов число. Фуниция fh(x) = f{z-h) называется сдвигом фунждии f{x). Пользуясь определен нем преобразования Фурье, показать, что Задача. Пусть функция f(z) имеет преобразование Фурье F(0> h - действительное число. Показать, что 3. Преобразование Фурье и ооерэции дифференцирования. Пусть абсолютно интегрируемая функция f(x) имеет производную f"(x), также абсолютно интегрируемую на всей оси Ох, так что /(я) стремится к нулю при |ж| -» +оо. Считая f"(x) гладкой функцией, запишем Интегрируя по частям, будем иметь Внеинтегральноеслагаемое обращается в нуль (так как, и мы получаем Таким образом, дифференцированию функции /(х) отвечает умножение ее образа Фурье ^П/] на множитель Если функция f(x) имеет глад*«е абсолютно интефируемые производные до порядка m включительно и все они, как и сама функция f(x), стремятся к нулю при то, интегрируя по частям нужное число раз, получим Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину и тем самым упрощает задачуинтегрирования некоторых видов дифференциальных уравнений. Так как преобразование Фурье абсолютно интегрируемой функции f^k\x) есть ограниченная функция от (свойство 2), то из соотношения (2) получаем для следующую оценку: ПРЕОБРАЗОВАНИЕ ФУРЬЕ Интеграл Фурье Комплексная форма интеграла Преобразование Фурье Косинус и синус преобразования Амплитудный и фазовый спектры Свойства Приложения Из этой оценки следует: чем больше функция f(x) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при. Замечание. Условие является достаточно естественным, поскольку обычная 1еория интегралов Фурье имеет дело с процессами, которые в том или ином смысле имеют начало и коней, но не продолжаются неограниченно с примерно одинаковой интенсивностью. 4. Связь между скоростью убывания функции f(x) при |z| -» -f оо и гладкостью ее преобразования Фурм. Предположим, что не только /(х), но и ее произведение xf(x) является абсолютно интегрируемой функцйей на всей оси Ох. Тогда преобразование Фурье) будет дифференцируемой функцией. Действительно, формальное дифференцирование по параметру £ подынтегральной функции приводит к интегралу который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и Таким образом, т. е. операция умножения f(x) на аргумент х переходит после преобразования Фурье в операцию t щ. Если вместе с функцией f(x) абсолютно интегрируемыми на всей оси Ох являются функции, то процесс дифференцирования можно продолжить. Получим, что функция имеет производные до порядка m включительно, причем Таким образом, чем быстрее функция f(x) убывает при тем более гладкой получается функция Теорема 2 (о сверле). Пусть- преобразования Фурье функций /,(ж) и f2(x) соответственно. Тогда причем двойной интеграл в правой части сходится абсолютно. Положим - х. Тогда будем иметь или, меняя порядок интегрирования, Функция называется сверткой функций и обозначается символом Формула (1) может быть теперь записана так: Отсюда видно, что преобразование Фурье свертки функций f\(x) и f2(x) равно умноженному на у/2ж произведению преобразований Фурье свертываемых функций, Замечание. Нетрудно установить следующие свойства свертки: 1) линейность: 2) коммутативность: §4. Приложения преобразования Фурье 1. Пусть Р(^) - линейный дифференциальный оператор порядка m с постоянными коэффициентами, Используя формулу для преобразования Фурье производных функции у(х), находим " Рассмотрим дифференциальное уравнение где Р - введенный выше дифференциальный оператор. Предположим, что искомое решение у(х) имеет преобразование Фурье у (О. а функция f(x) имеет преобразование /(£) Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси относительно откуда так что формально где символ обозначает обратное преобразование Фурье. Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида еЛ*, eaz cos fix, еах sin рх. Они не являются абсолютно интегрируемыми на оси -оо < х < 4-оо, и преобразование Фурье для них не определено, так что, строго говоря, применятьданный метод нельзя. Это ограничение можно обойти, если ввести в рассмотрение так называемые обобщенные функции. Однако в ряде случаев преобразование Фурье все же применимо в своей классической форме. Пример. Найти решение а = а(х, t) уравнения (а = const), при начальных условиях Это - задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение <р(х) точек сгруны, а начальные скорости отсутствуют. 4 Поскольку пространственная переменная х изменяется в пределах от -оо до +оо, подвергнем уравнение и начальные условия преобразованию Фурье по переменной х. Будем предполагать, что 1) функции и(х, t) и

Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:

• FT, DTF, DTFT - в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
• Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
• Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
• Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
• Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
• Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ - можно)
• Как по цифровой последовательности восстанавливают исходный сигнал

Я буду исходить из предположения что читатель понимает что такое интеграл , комплексное число (а так же его модуль и аргумент), свертка функций , плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака . Не знаете - не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”

Начать надо, наверное, с того что обычное преобразование Фурье - это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):

Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье - такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:

График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля - “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).

Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные - перемножаются. Первое выполняется легко, а второе - сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом - все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.

Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим:). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.

Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся - списком из семи пунктов справа:

Первое из этих свойств - линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:

Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике - это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.

Второе свойство преобразования Фурье - это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.

Третье свойство - растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.

Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот - поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.

Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi...pi) - нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра - для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).

Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии - остальная часть графика просто стремится к нулю (но, опять же, нулем не является).

Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:

Гребенка Дирака - это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T<<1. Фурье-образ этой функции - тоже гребенка Дирака, только с гораздо большим шагом 1/T и несколько меньшим коэффициентом (1/T). С математической точки зрения, дискретизация сигнала по времени - это просто поточечное умножение исходного сигнала на гребенку Дирака. Значение 1/T при этом называют частотой дискретизации:

Вместо непрерывной функции после подобного перемножения получается последовательность дельта-импульсов определенной высоты. При этом согласно свойству 5 преобразования Фурье, спектр получившегося дискретного сигнала есть свертка исходного спектра с соответствующей гребенкой Дирака. Несложно понять, что исходя из свойств свертки, спектр исходного сигнала при этом как бы “копируется” бесконечное число раз вдоль оси частот с шагом 1/T, а затем суммируется.

Заметим, что если исходный спектр имел конечную ширину и мы использовали достаточно большую частоту дискретизации, то копии исходного спектра не будут перекрываться, а следовательно и суммироваться друг с другом. Несложно понять что по подобному “свернутому” спектру будет легко восстановить исходный - достаточно будет просто взять компоненту спектра в районе нуля, “обрезав” лишние копии уходящие на бесконечность. Простейший способ это сделать - это домножить спектр на прямоугольную функцию, равную T в диапазоне -1/2T...1/2T и нулю - вне этого диапазона. Подобный Фурье-образ соответствует функции sinc (Tx) и согласно свойству 4, подобное умножение равнозначно свертке исходной последовательности дельта-функций с функцией sinc(Tx)

То есть с помощью преобразования Фурье мы получили способ легко восстановить исходный сигнал из дискретизированного по времени, работающий при условии что мы используем частоту дискретизации, по крайней мере вдвое (из-за наличия в спектре отрицательных частот) превышающую максимальную частоту присутствующую в исходном сигнале. Этот результат широко известен и называется “теорема Котельникова / Шеннона-Найквиста” . Однако, как несложно теперь (понимая доказательство) заметить, этот результат вопреки широко распространенному заблуждению определяет достаточное , но не необходимое условие для восстановления исходного сигнала. Все что нам требуется - это добиться того, чтобы интересующая нас часть спектра после дискретизации сигнала не накладывалась друг на друга и если сигнал достаточно узкополосный (имеет малую “ширину” ненулевой части спектра), то этого результата часто можно добиться и при частоте дискретизации намного ниже чем удвоенная максимальная частота сигнале. Подобная техника называется “undersampling” (субдискретизация, полосовая дискретизация) и довольно широко используется при обработке всевозможных радиосигналов. Например, если мы берем FM-радио действующее в полосе частот от 88 до 108 МГц, то для его оцифровки можно использовать АЦП с частотой всего 43.5 МГц вместо предполагающихся по теореме Котельникова 216 МГц. При этом, правда, понадобится качественный АЦП и хороший фильтр.

Замечу, что “дублирование” высоких частот частотами меньших порядков (алиасинг) - непосредственное свойство дискретизации сигнала, необратимо “портящее” результат. Поэтому если в сигнале в принципе могут присутствовать частоты высокого порядка (то есть практически всегда) перед АЦП ставят аналоговый фильтр, “отсекающий” все лишнее непосредственно в исходном сигнале (так как после дискретизации делать это уже будет поздно). Характеристики этих фильтров, как аналоговых устройств, неидеальны, поэтому некоторая “порча” сигнала при этом все равно происходит, и на практике из этого следует что наибольшие частоты в спектре, как правило, недостоверны. Чтобы уменьшить эту проблему, сигнал нередко сэмплируют с завышенной частотой дискретизации, ставя при этом входной аналоговый фильтр на меньшую полосу пропускания и используя только нижнюю часть теоретически доступного частотного диапазона АЦП.

Еще одно распространенное заблуждение, кстати, - это когда сигнал на выходе ЦАП рисуют “ступеньками”. “Ступеньки” соответствуют свертке дискретизированной последовательности сигналов с прямоугольной функцией ширины T и высоты 1:

Спектр сигнала при таком преобразовании умножается на фурье-образ этой прямоугольной функции, а у подобной прямоугольной функции это снова sinc(w), “растянутый” тем сильнее, чем меньше ширина соответствующего прямоугольника. Спектр дискретизированного сигнала при подобном “ЦАП” поточечно умножается на этот спектр. При этом ненужные высокие частоты с “лишними копиями” спектра обрезаются не полностью, а верхняя часть “полезной” части спектра, напротив, ослабляется.

На практике так, естественно, никто не делает. Существует много разных подходов к построению ЦАП, но даже в наиболее близких по смыслу ЦАП взвешивающего типа прямоугольные импульсы в ЦАП напротив выбираются по возможности короткими (приближающимися к настоящей последовательности дельта-функций) чтобы избежать излишнего подавления полезной части спектра. “Лишние” частоты в получившемся широкополосном сигнале практически всегда гасят, пропуская сигнал через аналоговый фильтр низких частот, так что «цифровых ступенек» нет ни «внутри» преобразователя, ни, тем более, на его выходе.

Однако вернемся обратно к преобразованию Фурье. Описанное выше преобразование Фурье, примененное к заранее дискретизированной последовательности сигналов называется преобразованием Фурье дискретного времени (DTFT). Спектр получаемый подобным преобразованием всегда 1/T-периодичен, поэтому спектр DTFT полностью определяется её значениями на отрезке }